Bem, estes dias têm sido um pouco corridos, ter que estudar a sério as coisas, e com um limite meio apertado, não é algo que se deva fazer. Mas, tirando esses mimimis da jogada, hoje eu queria escrever sobre uma coisa que eu gosto demais, e em parte motivado por algumas discussões com um amigo meu essa semana (calcular propagadores inversamente é uma porcaria ;p), que é o cálculo (ou análise, fica mais bonito) em variáveis complexas. Os resultados são bonitos, todo o conjunto na realidade, é muito interessante de estudar, e a aplicabilidade é variada, indo desde mecânica dos fluidos, teoria de circuitos, e outras coisas mais. Não tenho intenção de perder o meu tempo (e nem o seu, caro leitor ^^) rasgando seda com o assunto, por isso vou direto ao que eu quero expor. Se você não tem o menor saco com a matemática, ou não está com vontade de ler um texto provavelmente longo, pare por aqui.
______________________________________________________________
Um dos resultados que eu gosto muito deste tópico é o chamado Teorema dos Resíduos, que basicamente enuncia que a integral
\[\oint_C f(z) dz\]
depende somente das singularidades da função $f(z)$ que estão encerradas dentro do contorno suave $C$; Se $z_i$ são essas singularidades, então temos que
\[\oint_C f(z) dz=2\pi i\sum_{j=0}^n\text{Res}(f(z),z_j).\]
onde $\text{Res}(f(z),z_j)$ é o resíduo da função $f(z)$ no ponto $z_j$. Basicamente, o resíduo é o que sobra (daí o nome) quando definimos a série de Laurent da função $f(z)$ em torno do ponto $z_j$, e estudamos a convergência dessa série com integrais. É um resultado muito poderoso, pois mostra que efetuar essa integral independe totalmente da forma do caminho, bastando apenas saber se há singularidades dentro da região ou não.
Certo, mas e daí? Bem, uma aplicação legal desse teorema é o cálculo de integrais impróprias. Para exemplificar, podemos pegar a integral
\[I=\int_{-\infty}^{+\infty}\frac{1}{x^2+a^2}dx.\]
Essa é uma integral bem simples, tabelada, e tudo o mais. A primitiva da função no integrando é simples de calcular, dá (rabiscando um papel aqui) $\frac{1}{a}\text{arctg}(x/a)$. Aplicando os limites acima, vai dar um trabalhinho pra mostrar que eles dão $\pi/a$. Mas podemos usar o teorema dos resíduos pra calculá-la. A primeira coisa a fazer é considerar a versão complexa dessa integral:
\[I=\oint_C \frac{1}{z^2+a^2}dz,\]
onde podemos considerar o $C$ como decomposto abaixo:
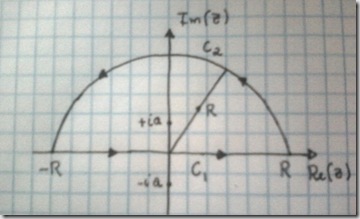
(Pois é, só um pretexto pra desenhar, e mal ;p) E então temos a integral
\[\oint_C \frac{1}{z^2+a^2}dz=\int_{C_1}\frac{1}{z^2+a^2}dz+ \int_{C_2}\frac{1}{z^2+a^2}dz.\]
A integral do lado esquerdo podemos calcular direto com o teorema dos resíduos: Como já devem ter notado, a função tem duas singularidades, que estão marcadas na figura. Como apenas uma delas está dentro do contorno $+ia$, e ele é a raiz da função, podemos calcular diretamente o resíduo da maneira
\[\text{Res}(f(z),+ia)=\lim_{z\rightarrow ia}(z-ia)\frac{1}{z^2+a^2}=\frac{1}{2ia}.\]
E vamos reservar esse resultado. A integral ao longo de $C_1$ é a integral que queremos calcular originalmente, se fizermos $R\rightarrow\infty$. Assim só nos resta calcular a integral em $C_2$. Mas, como estamos interessados no limite citado acima, podemos fazer uma estimativa da integral. Temos que
\[\left|\int_{C_2}\frac{1}{z^2+a^2}dz\right|\leq\int_{C_2}\left|\frac{1}{z^2+a^2}\right||dz|,\]
Bem, não entrando em detalhes demais, podemos parametrizar essa integral da forma $z=Re^{i\theta}$, e o lado direito torna-se a integral
\[\int_0^\pi\frac{R}{\sqrt{R^4+a^4+R^2a^2\cos 2\theta}}d\theta\approx\mathcal O(R^{-3})\]
Que, no limite $R\rightarrow\infty$, vai a zero. Então podemos dizer que a integral sobre $C_2$ vai pra zero, e temos que
\[\int_{-\infty}^{+\infty}\frac{1}{x^2+a^2}dx=2\pi i \text{Res}(f(z),ia)=\frac{\pi}{a}.\]
E Voilá! Obtemos exatamente o resultado que está tabelado.
“Poxa, isso é complicado pra caramba, prefiro usar um programa pra calcular isso, mimimi…” Bem, com esse exemplo parece complicado mesmo… Mas você pode calcular uma míriade de integrais, muitas das quais os programas mais modernos dão umas funções muito das suas esquisitas. E isso ainda quando dá para usar um programa.
Bem, aqui está. Eu poderia continuar dissertando horas e mais horas, mostrando como têm integrais realmente escrotas de se fazer, que são extremamente simples com esse método, mas acho que, se você chegou até aqui, seu interesse o levará a ler outras coisas. Basicamente, todo o livro de Cálculo em uma variável complexa que vale o papel impresso têm esse resultado, e de forma mais geral. E particular, eu cito os
__________________________
No mais, é só pela semana. See ya at the Next Savepoint o/


